[数据结构]-链表、栈、队列

链表

链表总结

链表是一种由节点（Node）组成的线性数据集合，每个节点通过指针指向下一个节点。它是一种由节点组成，并能用于表示序列的数据结构。

链表在进行循环遍历时效率不高，访问元素O(n)效率低，但是插入和删除时优势明显O(1)，且空间复杂度较高。链表结构可以充分利用计算机内存空间，实现灵活的内存动态管理。

数组的特点是：可以很方便地进行随机访问O(1)，但是增删元素O(n)比较耗时

选择数组还是链表要考虑业务对访问改和增删的要求

​

单链表

一个node只有一个指向下一个节点的指针，最后一个node指向null。一个指向链表头部的头节点。

java实现：

package structures;
​
public class myLinkedList<T> {
    public node head = null;
​
    class node {  //value不受类型限制
        T value;
        node next = null;
        public node(T value)
        {
            this.value = value;
        }
    }
​
    public boolean addNode (T v){
        node n = new node(v);
        if (head == null) {
            head = n;
            return true;
        }
        node tmp = head;
        while (tmp.next!=null)
        {
            tmp = tmp.next;
        }
        tmp.next = n;
        return true;
    }
    public boolean addNode(int index,T v) {//指定位置添加元素
        if (index>len())
            return false;
        int i;
        node cur=head;
        node pre=head;
        for(i=0;i<index;i++){
            pre=cur;
            cur=cur.next;
        }
        node newNode=new node(v);
        pre.next=newNode;
        newNode.next=cur;
        return true;
    }
​
    public int len (){
        int len=0;
        node tmp = head;
        while (tmp!=null)
        {
            tmp = tmp.next;
            len++;
        }
        return len;
    }
​
​
​
    public boolean removeNode (){
        if (head == null){
            return false;
        }
        if(len()==1){
            head=null;
            return true;
        }
        node cur = head;
        node pre = null;
        while (cur.next!=null)
        {
            pre=cur;
            cur = cur.next;
        }
        pre.next=null;
        return true;
    }
​
    public boolean removeNode(int index){//指定位置删除元素，需要两个指针，cur和pre
        if(head == null||index>=len())
        {
            return false;
        }
        int i;
        node cur=head;
        node pre=head;
        for(i=0;i<index;i++){
            pre=cur;
            cur=cur.next;
        }
        pre.next=cur.next;
        return true;
    }
​
​
    public void output (){
        node tmp=head;
        while(tmp!=null) {
            System.out.println(tmp.value);
            tmp=tmp.next;
        }
    }
​
​
    public static void main(String[] args)
    {
        myLinkedList list = new myLinkedList<String>();
        list.addNode("er");
        list.addNode("hj");
        list.addNode("j");
        list.addNode("hjk");
        list.output();
        list.removeNode(1);
        list.output();
        list.addNode(2,"456789");
        list.output();
    }
​
​
}

在尾部添加一个元素可以添加一个指向尾节点的指针last，oldlast=last，last=new node(v), oldlast.next=last.

双向链表

每个节点都有一个next指针指向后继，一个prev指针指向前者，能轻易的读取一个极点的前驱和后继，但是有更大的空间开销，在访问遍历等情况下有更高的复杂度，因为有更多的指针操作.

有头尾指针，双向遍历

​

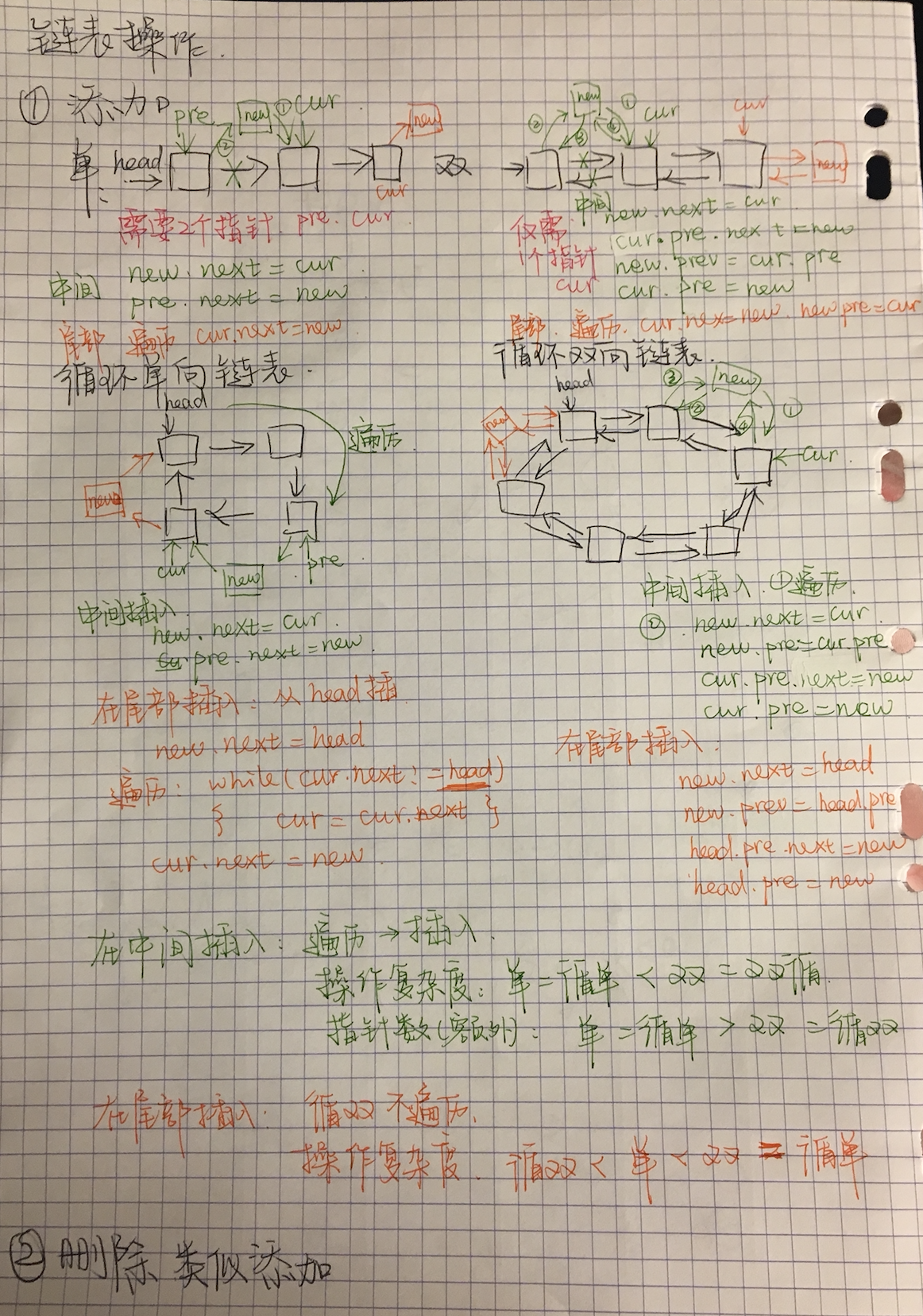
循环链表

分循环单链表和循环双链表，从表的任何一个节点出发都能找到表中的某个元素，双向循环链表很容易在尾部添加一个元素。

链表相关面试题

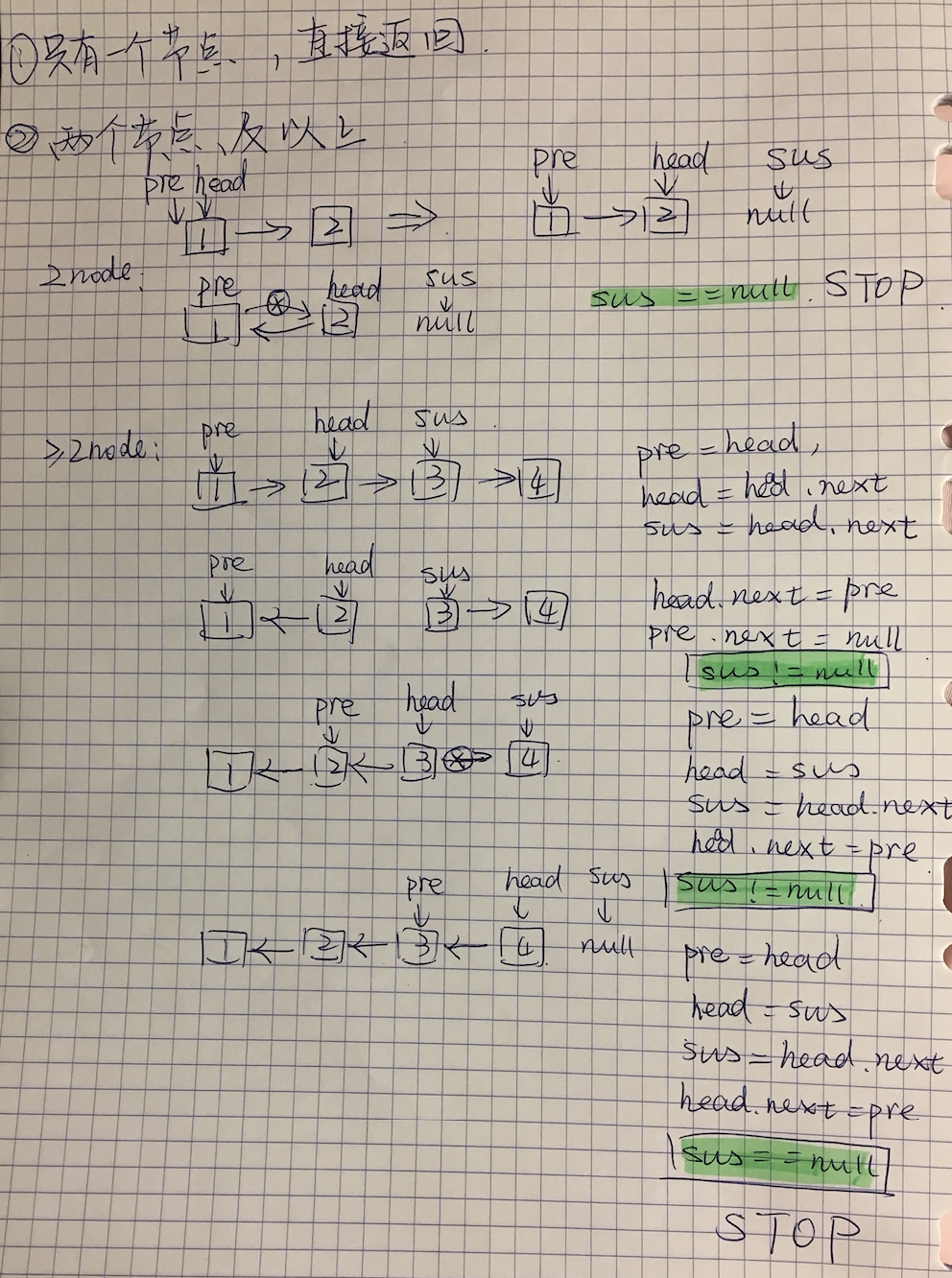
1.链表倒置（原地）O(n):

转置需要三个指针pre，head，sus，例如一个1->2->3的链表。第一步转置前两个节点：pre->1,head->2,sus->3，head.next->1, pre.next=null,此时:1<-2 3

第二步循环，若sus！=null， pre->2,head->3,sus->null,head.next->2.此时：1<-2<-3,且sus=null，终止。

public void reverse(){
       if(len()==1)
           return;
       node pre=head;
       head=head.next;
       node sus=head.next;
       head.next=pre;
       pre.next=null;
       while (sus !=null){
           pre=head;
           head=sus;
           sus=head.next;
           head.next=pre;
       }
   }

还可以新建一个链表，删除旧链表的元素同时加入新链表。空间复杂度更大一点。

2. 查找单链表的中间节点

采用快慢指针的方式查找单链表的中间节点，快指针一次走两步，慢指针一次走一步，当快指针走完时，慢指针刚好到达中间节点。

3. 查找倒数第k个元素

采用两个指针P1,P2，P1先前移K步，然后P1、P2同时移动，当p1移动到尾部时，P2所指位置的元素即倒数第k个元素 。

4.给定链表的头指针和一个节点指针，在O(1)时间删除该节点。[Google面试题]

分析：本题与《编程之美》上的「从无头单链表中删除节点」类似。主要思想都是「狸猫换太子」，即用下一个节点数据覆盖要删除的节点，然后删除下一个节点。但是如果节点是尾节点时，该方法就行不通了。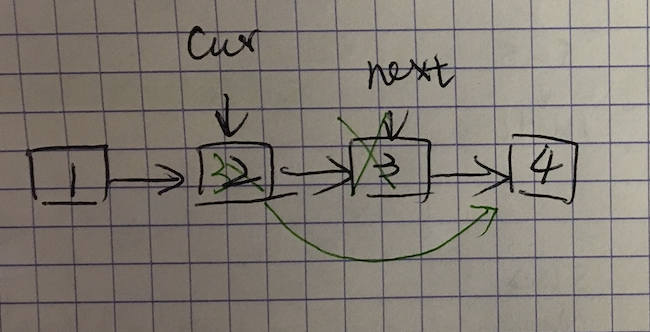

node next=cur.next;
cur.value=next.value;
cur.next=next.next;
delete next;

5. 判断单链表是否存在环

题目描述：输入一个单向链表，判断链表是否有环？

分析：通过两个指针，分别从链表的头节点出发，一个每次向后移动一步，另一个移动两步，两个指针移动速度不一样，如果存在环，那么两个指针一定会在环里相遇。

栈

栈是先进后出的数据结构LIFO，用数组实现栈的缺点是必须提前声明栈的大小，所以我们用链表来实现栈，可以动态分配栈的大小节约空间。
栈可用于DFS，深度优先遍历
java实现：

package structures;
import java.util.*;

public class myStack<T> {

    node first = null;
    int size=0;
    class node{
        node next=null;
        T value;
        public node(T v){
            this.value=v;
        }
    }

    public void push(T v){  //链表头作为栈头
        if(size==0){
            first= new node(v);
            size++;
            return;
        }
        node oldfirst = first;
        first = new node(v);
        first.next=oldfirst;
        size++;
    }

    public T pop(){
        if(size==0)
        {
            System.out.println("empty!");
            throw new EmptyStackException();
        }
        T value = first.value;
        first=first.next;
        size--;
        return value;
    }

    public boolean isEmpty(){
        return first==null;

    }

    public void output() {
        node tmp=first;
        while(tmp!=null)
        {
            System.out.println(tmp.value);
            tmp=tmp.next;
        }
    }
    public int size(){
        return size;
    }

    public static void main(String arg[]){
        myStack stack =new myStack();
        stack.push(1);
        stack.push(2);
        stack.push(3);
        stack.push(4);
        stack.output();
        System.out.println(stack.size());
        stack.pop();
        stack.pop();
        stack.pop();
        stack.pop();
        stack.pop();
        stack.output();
    }

}

用链表来实现栈，以链表头部作为栈顶部，压栈的时候创建一个新节点连接在头部前边。操作都在头部比较简单，没有很多的指针操作。

pop一个空栈抛出 EmptyStackException异常，同样的情况javascript的处理是返回一个undifined， php返回null。

队列

于栈相对，是先进先出FIFO的数据结构，也可以用数组或链表实现。可以用于实现广度遍历BFS。
java实现：

package structures;
import java.util.*;

public class myQueue<T> {

    node first = null;
    node last = null;
    int size=0;
    class node{
        node next=null;
        T value;
        public node(T v){
            this.value=v;
        }
    }

    public void enqueue(T v){  //链表头作为栈头
        if(size==0){
            node n= new node(v);
            first = n;
            last = n;
            size++;
            return;
        }
        node oldlast = last;
        last = new node(v);
        oldlast.next = last;
        size++;
    }

    public T dequeue(){
        if(size==0)
        {
            System.out.println("empty!");
            throw new NoSuchElementException();
        }
        T value = first.value;
        first=first.next;
        size--;
        return value;
    }

    public boolean isEmpty(){
        return size()==0;

    }

    public void output() {
        node tmp=first;
        while(tmp!=null)
        {
            System.out.println(tmp.value);
            tmp=tmp.next;
        }
    }
    public int size(){
        return size;
    }

    public static void main(String arg[]){
        myQueue<Integer> queue =new myQueue<Integer>();
        queue.enqueue(1);
        queue.enqueue(2);
        queue.enqueue(3);
        queue.enqueue(4);
        queue.output();
//        System.out.println(queue.size());
        queue.dequeue();
        queue.output();


    }

}

队列用一个带有头指针和尾指针的链表实现，入队列的时候我们从尾部添加元素。出队列时从头指针删除元素。

当删除一个空队列的元素时，抛出NoSuchElementException异常。

栈和队列相关面试题

1.用两个栈实现一个队列

翻译过来就是使用两个栈定义一种先放入的元素，最先被取出的数据结构。
此题应考虑到两种情况，首先最简单的一种情况，假设有 1，2，3，4，5 个元素依次进入自定义的队列，再依次取出。由于是进栈操作都进行完了才进行出栈操作，所以我们只需在元素出队时，将进栈元素倒入另一个空栈中即可。示意图如下：

再一种情况是，如果 add poll 操作是交替进行的，那么如何保证数据结构先进先出的定义呢？比如先放入 1，2，3然后要进行一次取出操作取出 1，随后在进行 add 操作放入4，5，这种情况下如何操作两个栈，才能保证之后再取出的时候元素为 2，3，4，5 顺序？实际上我们只需要保证一下两点就可以：

• 无论如果 StackA（最开始add元素的那个栈） 要往 StackB 中压入元素，那么必须选择一次性全部压入。
• 无论什么时候从队列中取元素，必须保证元素是从 StackB 中 pop 出的，也就是说，当 StackB 不为空的时候绝不能再次向 StackB 中压入元素。

java实现：

package structures;
/**
 * @author jiaxuehui
 * @version 1.0
 * @Description 用两个栈实现一个队列
 * @Date 01/11/2018 1:31 PM
 */
public class Stack2Queue<T> {
    myStack<T> sin = new myStack();
    myStack<T> sout = new myStack();
    public void enqueue(T v){//enqueue只需在sin栈中放入元素
        sin.push(v);
    }

    public T dequeue(){//当sout中还有元素时，从sout中出队列，当sout为空时才可以从sin中出队列到sout中，以避免顺序混乱
        if (sin.isEmpty() && sout.isEmpty()){
            return null;
        }
        if(sout.isEmpty()){
            while (!sin.isEmpty()){
                sout.push(sin.pop());
            }
        }
        return sout.pop();
    }

    public void ouput(){//先输出sout的值，在输出sin的元素，用一个临时栈tmp存放sin的值并输出，再依次压回sin中。
        if (sin.isEmpty() && sout.isEmpty()){
            return;
        }
        sout.output();
        myStack<T> tmp =new myStack();
        while (!sin.isEmpty()){
            tmp.push(sin.pop());
        }
        tmp.output();
        while (!tmp.isEmpty()){
            sin.push(tmp.pop());
        }
    }
    public static void main(String arg[]){
        Stack2Queue<Integer> queue = new Stack2Queue<>();
        queue.enqueue(1);
        queue.enqueue(2);
        queue.enqueue(3);
        queue.enqueue(4);
        queue.dequeue();

        queue.ouput();

    }
}

2.两个队列实现一个栈

队列不能逆序，需要换一种思路，用两个队列交替输出。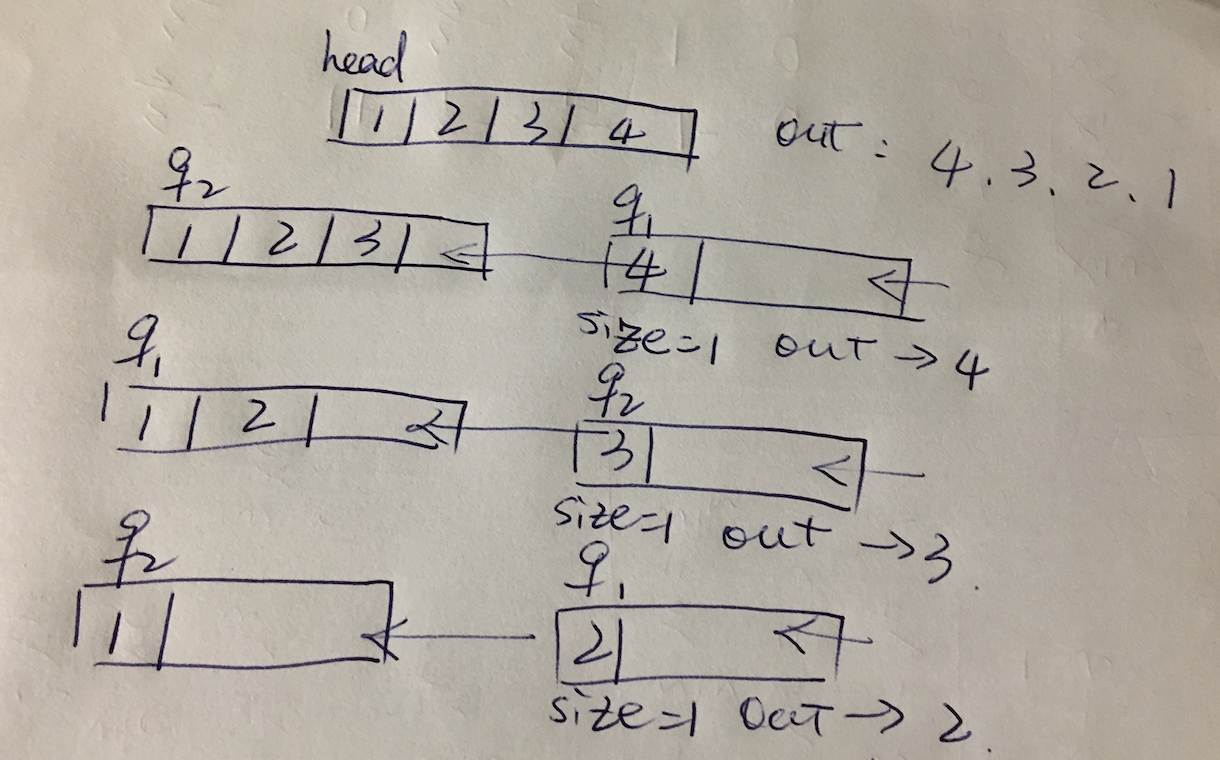

java实现：

package structures;
/**
 * @author jiaxuehui
 * @version 1.0
 * @Description 用两个队列实现一个栈
 * @Date 01/11/2018 1:31 PM
 */
public class Queue2Stack<T> {
    myQueue<T> q1 = new myQueue();
    myQueue<T> q2 = new myQueue();
    public T pop(){
        if(q1.isEmpty()&&q2.isEmpty())
        {
            return null;
        }
        if(!q1.isEmpty()) {
            while (q1.size() != 1) {
                q2.enqueue(q1.dequeue());
            }
            return q1.dequeue();
        }
        if (!q2.isEmpty()){
            while (q2.size() != 1) {
                q1.enqueue(q2.dequeue());
            }
            return q2.dequeue();
        }
        return null;
    }
    public void push(T v){
        if (q1.isEmpty()&&q2.isEmpty() || q2.isEmpty()){
            q1.enqueue(v);
        }
        if(!q2.isEmpty())
            q2.enqueue(v);
    }
    public void output(){
        if(!q1.isEmpty())
            q1.output();
        if(!q2.isEmpty())
            q2.output();
    }
    public static void main (String arg[]){
        Queue2Stack stack = new Queue2Stack();
        stack.push(1);
        stack.push(2);
        stack.push(3);
        stack.pop();
        stack.push(4);
        stack.push(5);
        stack.push(6);
        stack.pop();
        stack.pop();
        stack.output();

    }
}

3.给定一个栈的输入序列，判断输出序列是否合法

用一个循环来实现，假设输入序列1，2 3，4，5 输出序列4，3，5，1，2。我们依次读取输出序列的值，若在栈顶，就出栈，否则继续压栈直到压入该数字。如果输入已经全部压栈，仍没有栈顶元素等于改元素，则该输入不合法。总之查看每个输出的可能性。
如图：

java实现：

package algos;
import java.io.IOException;
import java.util.*;
import java.io.InputStream;
/**
 * @author jiaxuehui
 * @version 1.0
 * @Description 分别给定入栈序列和出栈序列，然后判断出栈序列是否合法
 * @Date 01/11/2018 1:31 PM
 */
public class IsRightStackOutput {
    public boolean isRightStackOutput(int[] input, int[] res, int n){
        int i;
        int j=1;
        int[] tmp = new int[n];
        Stack<Integer> stack = new Stack<>();
        stack.push(input[0]);
        for(i=0;i<res.length;i++){
            if (!stack.empty()&&stack.peek() == res[i]) {
                System.out.println(stack.pop());
            }
            else {
                if(j==n)
                    return false;
                while (j<n){
                    if(input[j] == res[i]){
                        stack.push(input[j]);
                        j++;
                        System.out.println(stack.pop());
                        break;
                    }
                    else {
                        stack.push(input[j]);
                        j++;
                    }
                }

            }
        }
        return true;
    }

    public static void main(String arg[]){
        Scanner sc = new Scanner(System.in);
        System.out.println("length of sequence:");
        int n = sc.nextInt();
        int[] input = new int[n];
        int[] res = new int[n];
        int i;
        System.out.println("your input sequence:");
        for(i=0;i<n;i++){
            input[i]=sc.nextInt();
        }
        System.out.println("your result sequence:");
        for(i=0;i<n;i++){
            res[i]=sc.nextInt();
        }
        IsRightStackOutput is = new IsRightStackOutput();
        System.out.println(is.isRightStackOutput(input, res, n));
    }

}

部分参考图片和解释来自于https://juejin.im/post/5b5536825188251af6622815